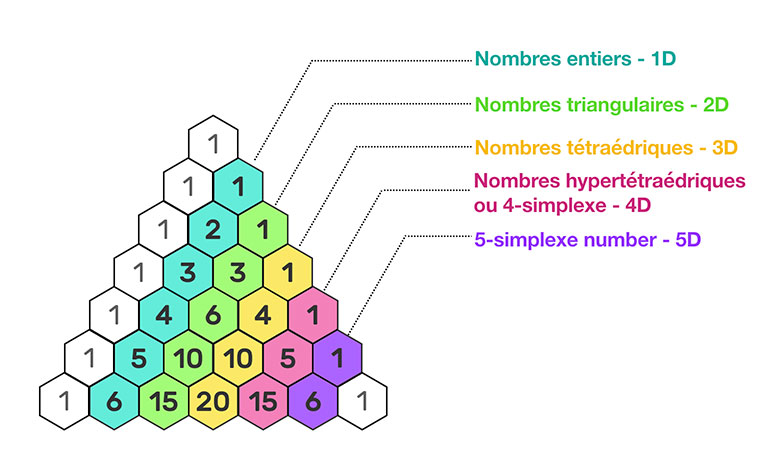
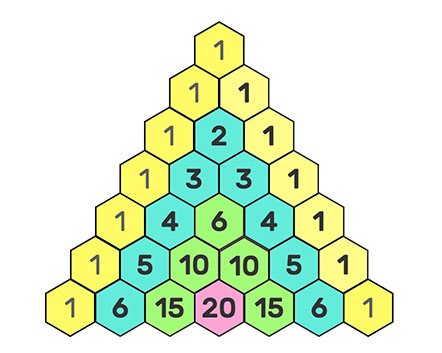
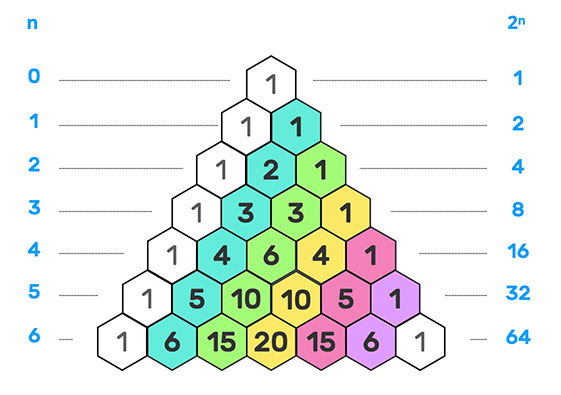
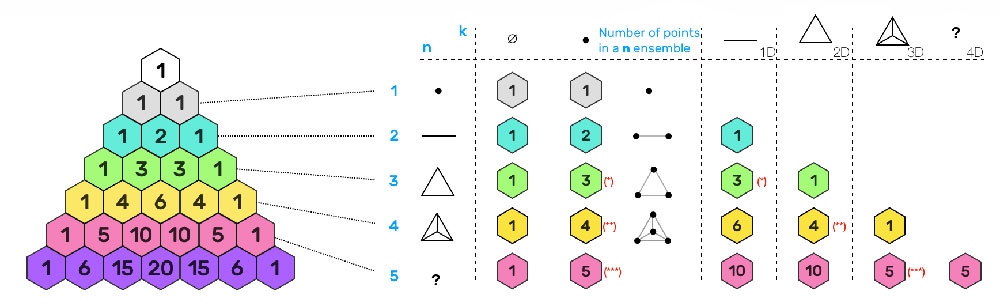
Les 3 points-clefs
OOrigine et Caractéristiques du Triangle :
Le triangle, une forme géométrique fondamentale, détient une place centrale en mathématiques et culture. Dès l'Égypte ancienne, il était utilisé pour mesurer terres et constructions. Les Grecs, notamment Euclide, l'ont approfondi dans "Les Éléments". En architecture, les pyramides égyptiennes sont des exemples marquants de son utilisation. Le triangle se caractérise par trois côtés, sommets et angles, et la somme de ses angles intérieurs est toujours de 180 degrés. Il existe en diverses formes, y compris rectangles, équilatéraux, isocèles et scalènes.
GGéométrie et Symbolisme du Triangle :
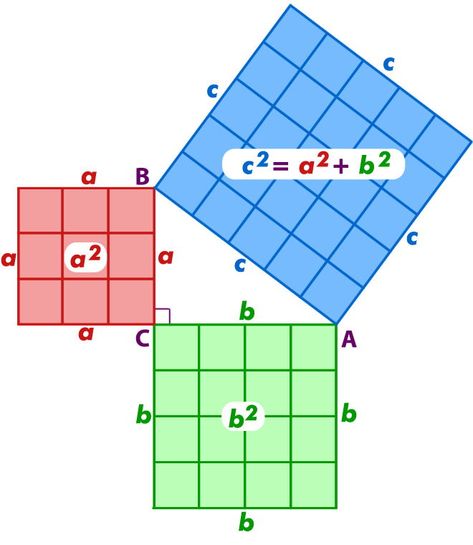
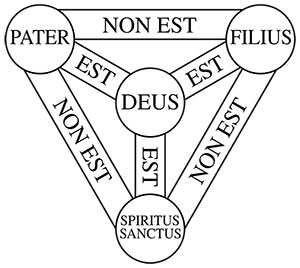
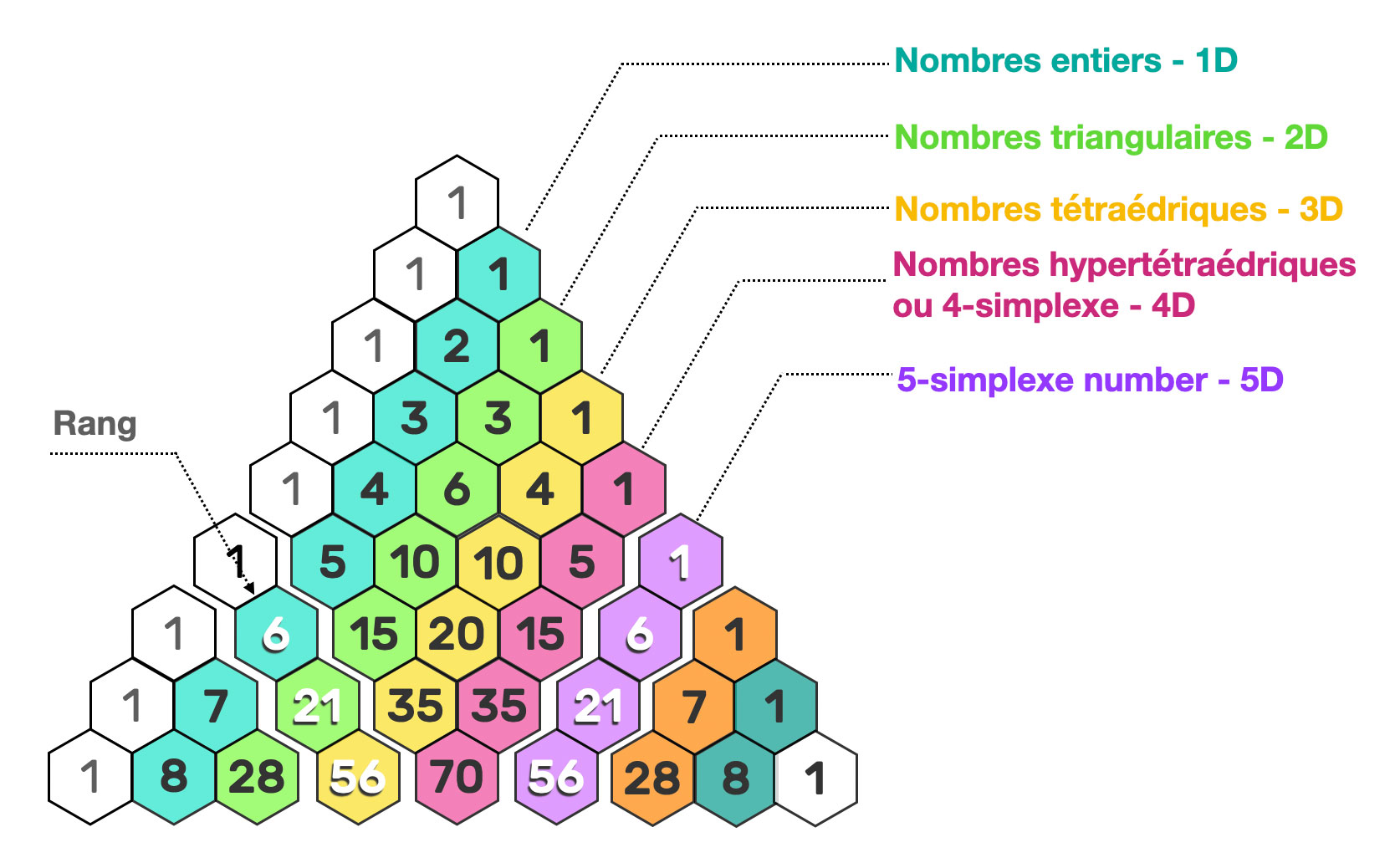
Le triangle est plus qu'une simple forme, il symbolise la loi ternaire et la trinité dans divers contextes culturels et spirituels. Il représente des notions de spiritualité, divinité et stabilité. En géométrie sacrée, il est une "figure mère", fondamentale à l'alphabet de la géo-numérologie. Il se relie aussi aux cycles temporels, comme les phases de la journée et les mois de l'année. Le triangle de Pythagore illustre des relations numériques fondamentales, affirmant l'union entre mathématiques et symbolisme.
PTriangle en Psychologie et Ésotérisme :
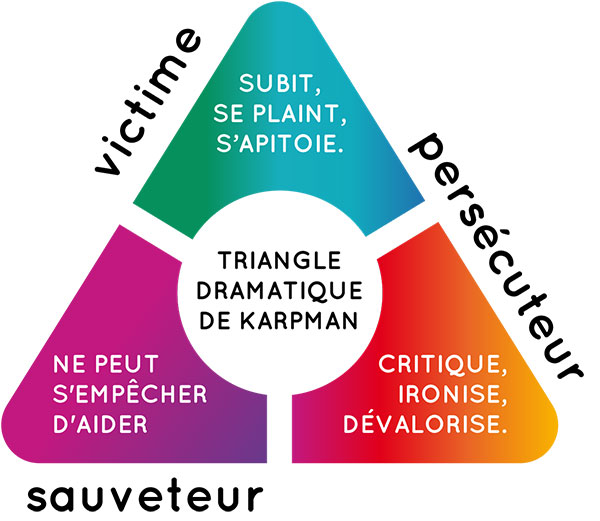
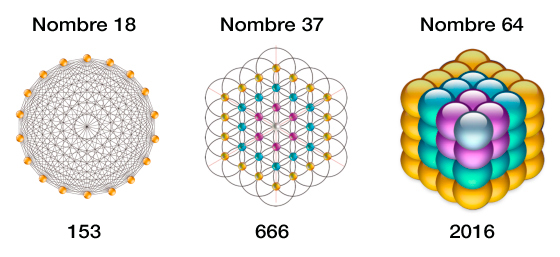
Le triangle se manifeste aussi en psychologie, illustré par le triangle de Karpman et la pyramide de Maslow. Karpman explique les dynamiques relationnelles dysfonctionnelles, tandis que Maslow hiérarchise les besoins humains. Ésotériquement, le triangle apparaît dans la Bible avec des significations profondes, liées à des nombres comme 153 et 666. Ces nombres révèlent des connexions divines et sont essentiels pour décrypter des mystères bibliques. Le Tarot de Marseille, comportant des éléments liés aux nombres triangulaires, relie aussi le triangle à des dimensions supérieures de compréhension.