📖 Sommaire
De la Numérologie à la Géométrie Sacrée
La Géométrie sacrée est l'expression géométrique dont se pare la source de vie pour se manifester dans le monde physique. Découvrez comment les nombres se transforment en formes archétypes et révèlent les mystères de l'univers.
L'Art du Trait ou l'Esprit de Géométrie
L'art du trait révèle la structure invisible de l'univers
Essence de la Géométrie Sacrée
La géométrie sacrée est une branche de la géométrie qui étudie les formes géométriques et les symboles qui ont une signification spirituelle et symbolique dans différentes traditions religieuses, philosophiques et ésotériques.
Elle est considérée comme sacrée car elle est associée à des principes universels qui sont censés régir l'univers et la vie elle-même, et qui peuvent aider les individus à atteindre un état de conscience supérieur.
Contrairement à d'autres symboles tels que les symboles chimiques ou les notes de musique, le symbolisme géométrique est le seul qui correspond à la nature elle-même, à la structure de l'univers.
Le symbolisme ésotérique est un véritable langage universel, reflétant de manière absolue la nature et ses lois, plutôt que d'être une simple invention.
La géométrie agit comme un pont reliant les nombres et les symboles. Bien que toutes les formes géométriques ne soient pas symboliques, dans de nombreux cas, voire tous les cas, le symbole est inspiré de la géométrie.
Les formes et les symboles de la géométrie sacrée sont souvent utilisés dans des pratiques spirituelles telles que la méditation, la prière et la guérison, ainsi que dans des domaines tels que l'architecture, l'art et la musique pour créer des espaces et des œuvres qui sont en harmonie avec ces principes universels.

L'idée du mot "idée" vient du latin "idea", signifiant "type de choses". Ce terme a été emprunté au grec "ἰδέα", qui signifie littéralement "forme visible, aspect", mais qui a évolué pour signifier "forme distinctive, espèce", dérivé du verbe "voir" ("εἶδος").
Le Pont entre l'Esprit et la Matière
La pensée est ce fil invisible qui dégage l’idée de la forme, révélant le lien intime entre l’Esprit et la Matière, entre l’invisible et le visible. Dans ce processus, le symbole joue un rôle fondamental : il ne se contente pas de représenter, il suggère et ouvre vers l’idée qu’il incarne.
Les symboles de la géométrie sacrée naissent de motifs simples — le cercle, le carré, le triangle — qui, par combinaison et superposition, donnent naissance à des structures plus complexes et porteuses de sens. Ces formes de base ne sont pas de simples constructions géométriques : elles sont des archétypes universels, reflets visibles des lois invisibles.
La géométrie sacrée repose sur des principes immuables comme la symétrie et l’isomorphisme, qui appartiennent autant aux mathématiques qu’à la structure profonde de l’univers. Ces lois d’harmonie, que l’on retrouve dans la nature, l’art et l’architecture sacrée, deviennent en Géo-numérologie des clés de compréhension de la psyché humaine et du cosmos.
Pour tracer géométriquement les 29 symboles de la Géo-numérologie, j’ai dû recourir à des grilles de construction communes. Cette méthode m’a permis de les comparer entre eux et de révéler les affinités cachées qui les relient. Ainsi, les principes mêmes de la géométrie sacrée — symétrie, proportion, résonance et correspondance — se sont imposés naturellement pour construire un système cohérent et vivant, capable de refléter la dynamique de l’âme et son inscription dans l’univers.
Ces symboles ne sont donc pas de simples figures : ils sont de véritables ponts, reliant l’ordre invisible des idées à l’ordre visible des formes, et ouvrant à une compréhension unifiée de l’homme et du cosmos.
Principes Universels
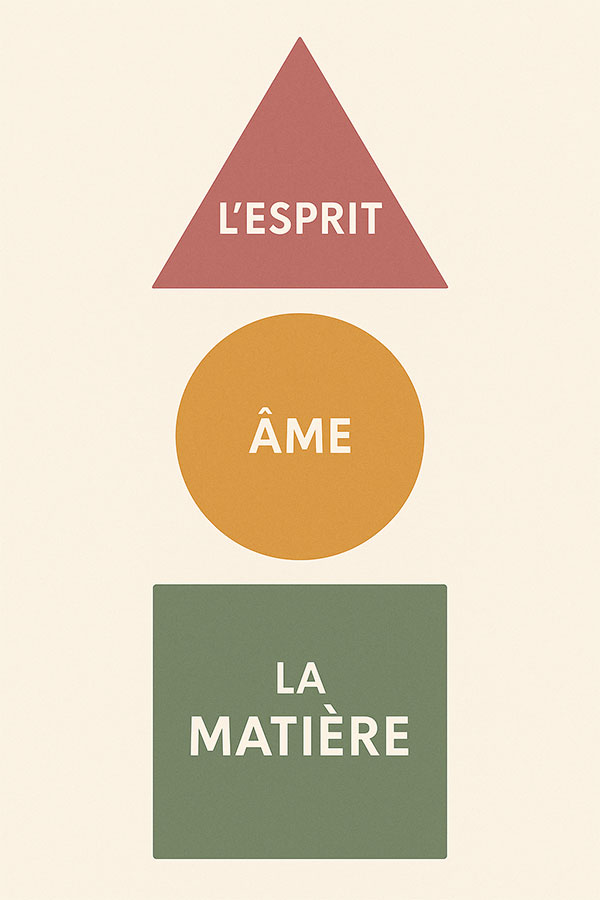
L'esprit (triangle) anime (cercle) la matière (carré)
selon la loi ternaire de la manifestation.
La Loi de l'Analogie
Matyla C. Ghyka, dans l'avant-propos de son ouvrage sur Le Nombre d'Or, précise que les termes de symétrie et d'analogie sont intimement liés par la notion de proportion telle que l'entendaient les anciens.
Pour qualifier la symétrie et la proportion de l'art méditerranéen, il décrit :
de procédés graphiques qui (...) aboutissent à reproduire des tracés dans lesquels le thème de l'ensemble se réfléchit, se reproduit, suivant un certain rythme plus ou moins voilé, dans chacune des parties. Loi de l'analogie, de la répétition de la forme fondamentale, de l'identité dans la variété, du Même et du Semblable.
Toute la matière est le résultat de combinaisons géométriques entre les atomes, de même que tous les symboles de la géonumérologie proviennent de la combinaison de quelques formes archétypes, aussi nommées figures mères.
Symétries Axiales et Centrales
Les propriétés géométriques des figures mères
révèlent leur perfection mathématique.
Les trois Figures mères
🔺 Triangle Équilatéral
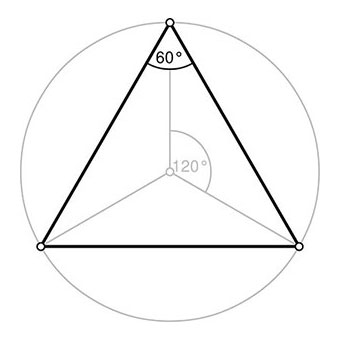
Symétrie axiale : Le triangle équilatéral a trois axes de symétrie qui sont les médianes reliant chaque sommet au milieu du côté opposé. Chaque axe de symétrie divise le triangle en deux parties symétriques.
Symétrie centrale : Le triangle équilatéral possède un centre de symétrie, qui est également le centre de gravité et l'intersection des trois médianes. La symétrie centrale divise le triangle en trois parties symétriques.
Seuls les polygones réguliers dont l'angle au sommet est un sous-multiple de 360 peuvent satisfaire aux conditions d'un pavage régulier.
Nb d'angles : 3
⦨ externe 120 (red°=3)
⦨ interne 60° (red°=6)
⬟ Hexagone Régulier
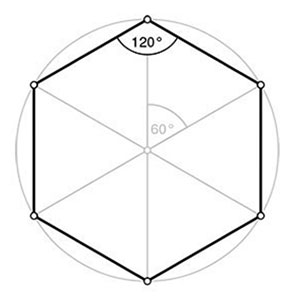
Symétrie axiale : L'hexagone régulier a six axes de symétrie qui passent par le centre de l'hexagone et qui relient les sommets opposés. Chaque axe de symétrie divise l'hexagone en deux parties symétriques.
Symétrie centrale : L'hexagone régulier possède un centre de symétrie qui est également le centre de gravité, l'intersection des trois diagonales et le milieu de chaque côté. La symétrie centrale divise l'hexagone en six parties symétriques.
Nb d'angles : 6
⦨ externe 60 (red°=6)
⦨ interne 120° (red°=3)
Le côté de l'hexagone étant égal au rayon, la circonférence du cercle sera de 3 cm pour un rayon 0,5 cm, ce qui est très proche de la valeur exacte de la circonférence C = 2Πr, soit 3,14.
C'est la raison pour laquelle on considère l'hexagone comme un "nombre circulaire".
◻ Carré
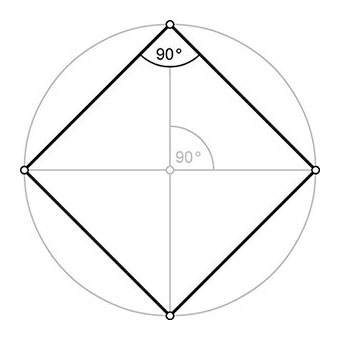
Symétrie axiale : Le carré a quatre axes de symétrie, qui sont les deux diagonales et les deux droites reliant les milieux des côtés opposés. Chaque axe de symétrie divise le carré en deux parties symétriques.
Symétrie centrale : Le carré possède un centre de symétrie qui est également le centre de gravité, l'intersection des diagonales. La symétrie centrale divise le carré en quatre parties symétriques.
Nb d'angles : 4
⦨ externe 90° (red°=9)
⦨ interne 90° (red°=9)
Vous remarquerez que la réduction pythagoricienne appliquée aux angles reproduit la série des valeurs secrètes des nombres... les fameux nombres 369.
120° → 1+2+0 = 3
60° → 6+0 = 6
90° → 9+0 = 9
L'Art de Remplir le Plan
Une tessellation régulière couvre une surface
sans laisser de vide ni chevauchement.
Les trois pavages du plan
Les Trois Pavages Universels
Une tessellation régulière est un motif réalisé en répétant un polygone régulier de manière à couvrir une surface sans laisser de vide.
Il n'y a que trois pavages réguliers, ou façons de remplir le plan euclidien avec des polygones réguliers :
- Le triangle équilatéral - Pavage triangulaire
- Le carré - Pavage carré
- L'hexagone régulier - Pavage hexagonal
Le pentagone ne permet pas de remplir totalement le plan. Il n'est pas à considérer comme une « figure mère ».
D'autre part son axe de symétrie situé au sommet ne lui confère pas un caractère d'isométrie. Son étude relève d'une approche polygonale ou symbolique.
🔺 Pavage Triangulaire
Le pavage des triangles équilatéraux est le plus dense des trois. Chaque sommet se relie à six voisins, créant un champ vibrant, presque ondulatoire.
Il exprime la dynamique de l’esprit : l’expansion de la pensée, la ramification infinie des idées, la force vive qui anime la conscience.
Dans la géométrie sacrée, ce réseau triangulaire est associé au feu, à l’énergie ascendante, au principe actif.
⬟ Pavage Hexagonal
Le pavage des hexagones réguliers est une merveille d’harmonie : il résulte de l’alliance du triangle et du cercle, et il remplit l’espace avec une élégance naturelle.
C’est la figure que la nature choisit spontanément – on la retrouve dans les alvéoles d’abeilles, les réseaux cristallins ou les molécules.
Il représente la synthèse vivante, l’équilibre entre l’esprit et la matière, le principe d’organisation du vivant.
◻ Pavage Carré
Le pavage des carrés incarne la stabilité, l’ordre et la structure.
Il est le sol de la maison, la pierre de fondation, le champ cultivé. Symbole de la matière et de la réalité tangible, il est le support où l’esprit vient s’incarner.
Sa régularité parfaite reflète la loi, la mesure et le devoir, rappelant que toute construction repose sur une base solide.
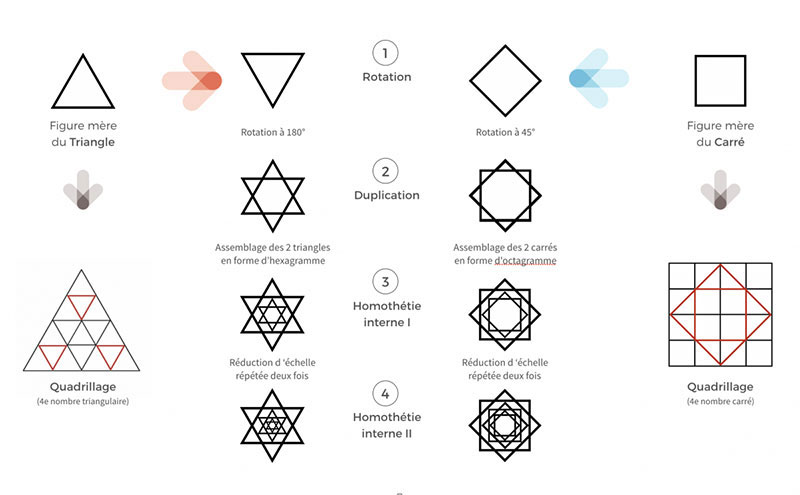
Duplication, Rotation et Homothétie
Les trois mouvements fondamentaux
de la géométrie créatrice.
Les trois mouvements de base de la Géométrie
🔺 Duplication (ou translation)
La duplication est une transformation qui crée une copie identique d'une figure à une distance donnée de la figure originale.
La figure dupliquée est donc une réplique exacte de la figure originale, mais située à un autre endroit de l'espace.
⬟ Rotation (ou pivotement)
La rotation est le mouvement qui tourne une figure autour d'un point central, appelé centre de rotation.
Chaque point de la figure reste à la même distance du centre de rotation, mais change de position en fonction de l'angle de rotation.
◻ Homothétie (ou changement d'échelle)
L'homothétie est une transformation qui change la taille d'une figure sans changer sa forme.
Elle se produit lorsqu'une figure est agrandie ou réduite proportionnellement par rapport à un point fixe appelé centre d'homothétie.
Quant au maître de notre temps, il ne pouvait concevoir aucune rosace, aucun pilier, aucun détail gothique sans une figure originelle inspirée, certes, par sa fantaisie créatrice mais construite selon les mêmes principes de la répétition, du rétrécissement, de la division et du basculement des simples figures de base, telles les figures-mères.
— Franz Rziha ~ étude sur les marques de tailleurs de pierre
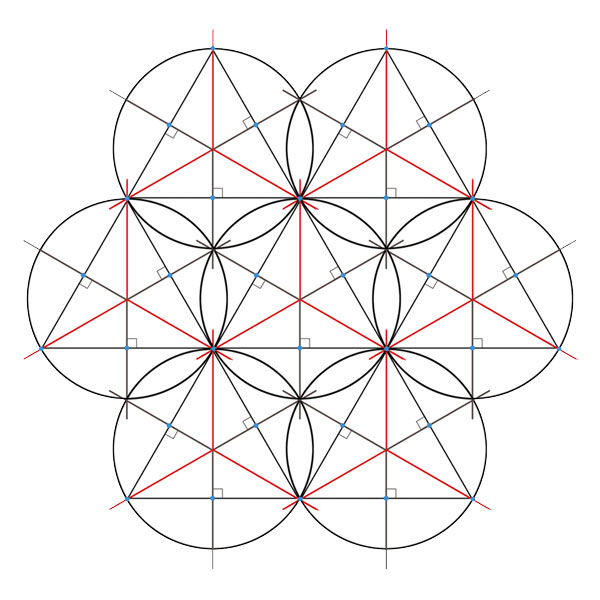
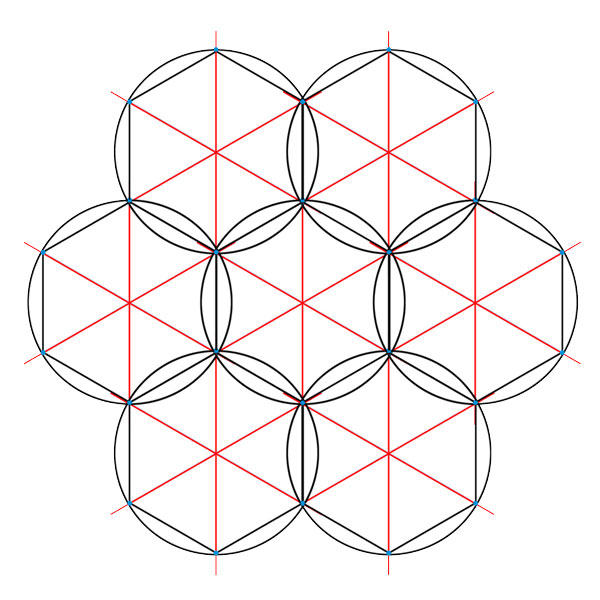
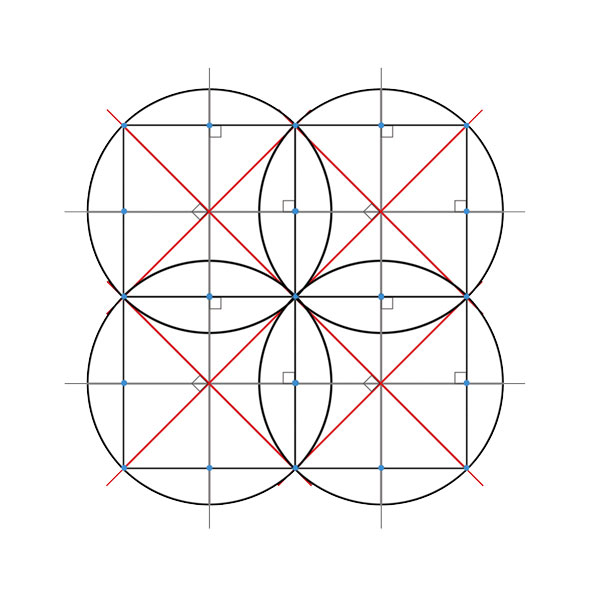
Réseaux, Treillis ou Champs Morphogénétiques
Les grilles de construction découvertes par Franz Rziha
révèlent l'organisation secrète des bâtisseurs.
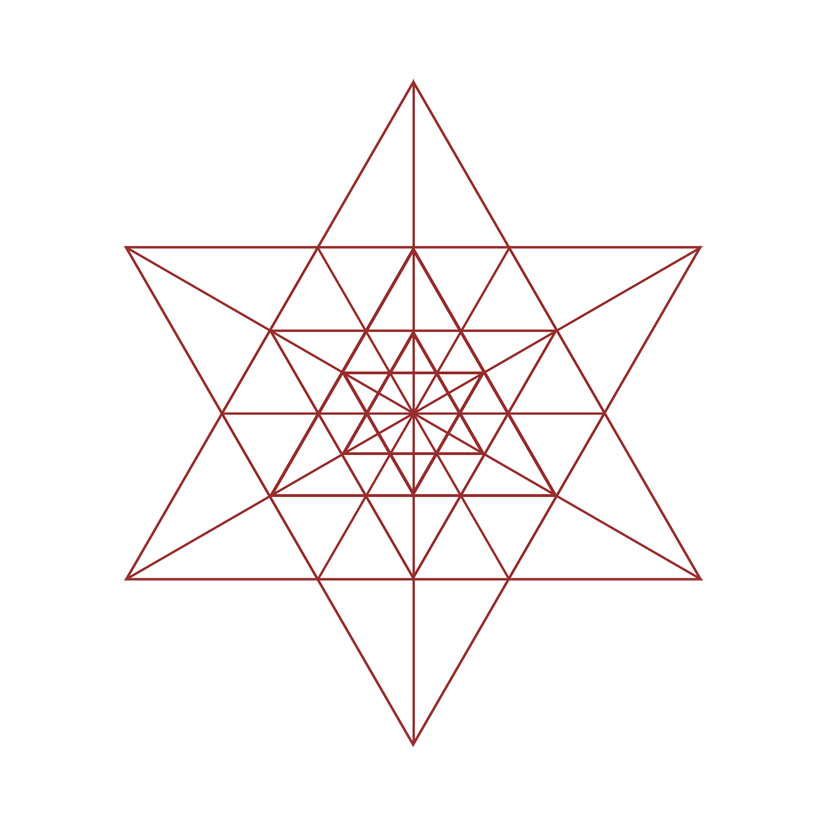
Le quadrillage de la quadrature montre parfaitement que le carré extérieur est deux plus grand que celui à l'intérieur. Il suffit de compter les petits carrés et les petits triangles à l'intérieur de chaque. Ce procédé est connu comme étant la duplication du carré.
La Découverte de Franz Rziha
Dans Le Nombre d'or Matila Ghyka fait référence à « l'immense travail » de l'architecte autrichien Franz Rziha qui « parait avoir trouvé la clef mathématique et logique ».
Ses études faites sur la Bauhûtte, fédération des tailleurs de pierre sous l'empire germanique au XVème et au XVIème siècle, montrent que tous les signes laissés par les ouvriers et maîtres sur les monuments dérivent de quatre matrices types ou réseaux, de complexité croissante, que Rziha appelle :
- Quadrature
- Triangulation
- Rosace
Ces trois grilles, et leurs déclinaisons en trilobe (triangle et cercle) et quadrilobe (triangle et carré), servent de patterns pour la disposition des unités d'un nombre et permettent ainsi d'obtenir son image.
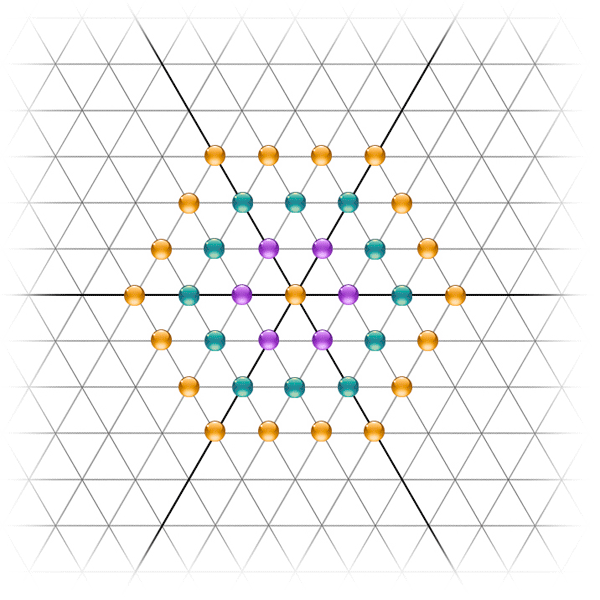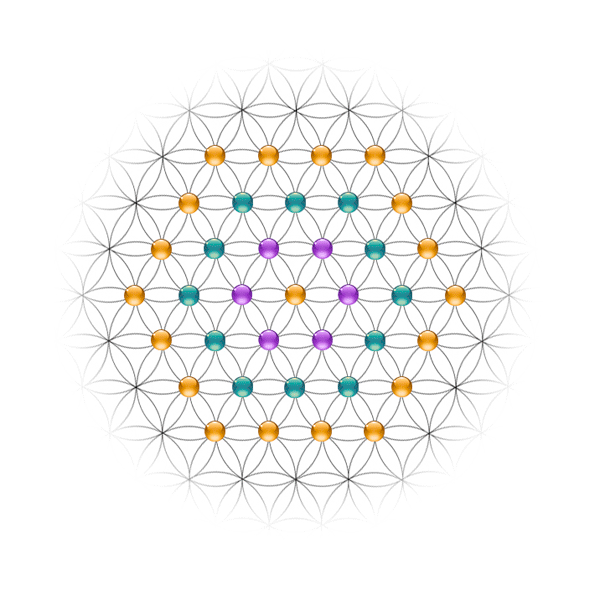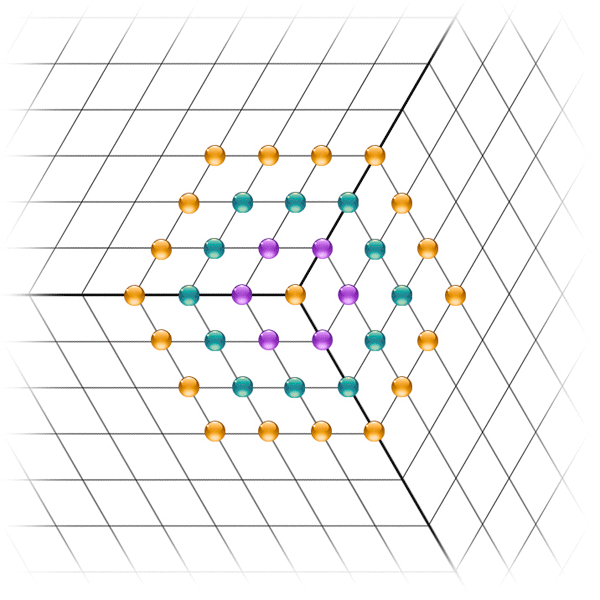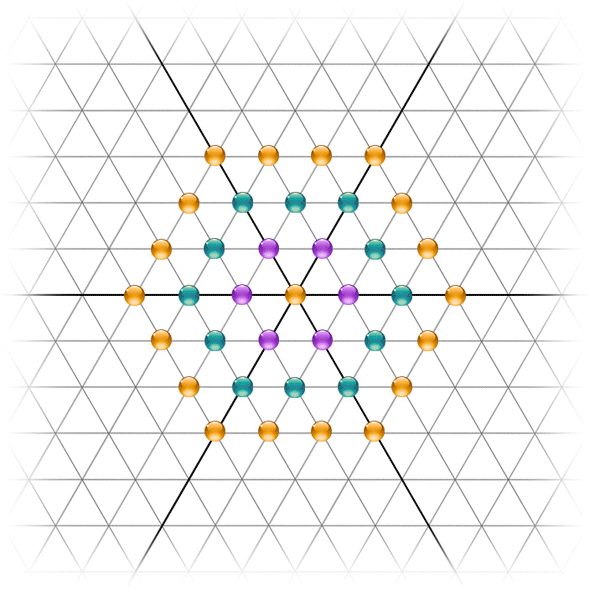
🔺 La Triangulation
L'Esprit
La Sphère Intellectuelle
Symbole pythagoricien de la Sagesse, le triangle est aussi le symbole chrétien de la divinité et en particulier de la Trinité à travers les trois Personnes : Le Père, le Fils et le Saint-Esprit.
Le triangle évoque également la loi ternaire universelle : temps (passé, présent et futur), espace en trois dimensions, les 3 règnes (minéral, végétal et animal), etc.
Il est associé aux qualités de l'esprit (thèse, antithèse et synthèse).
Symbole du « corps mental »
⬟ La Rosace
L'Ame

La Sphère Émotionnelle
Symbole du Tout, de l'éternité, le cercle représente également le néant tant qu'il n'est pas animé par un point central.
Symbole du « corps astral », il évoque aussi bien l'âme, que le « corps émotionnel » ou le « corps Subtil ». Tout est une question de proportion.
Dans la poésie de la Renaissance en général, le cercle était un symbole de la perfection et est un symbole de l'âme humaine.
Symbole du « corps astral »
◻ La Quadrature
Le Corps
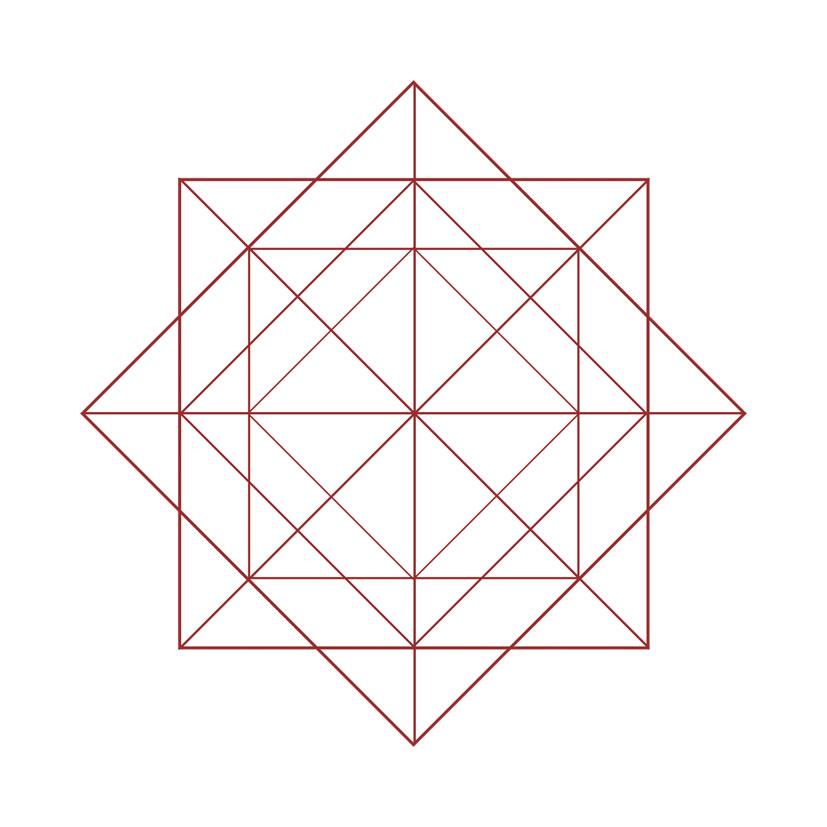
La Sphère Vitale
Le carré est un symbole du monde manifesté. Il évoque les 4 éléments (Feu, Air, Eau et Terre), les 4 états de la matière (ignée, gazeuse, liquide et solide) ou les 4 points cardinaux (Nord, Sud, Est et Ouest).
Il est donc une image de l'espace et de la matière, de concrétisation et de stabilité.
Le carré représente l'ancrage dans la réalité physique et la manifestation terrestre de l'esprit.
Symbole du « corps physique »
Nombres Cubiques : Une Vision Géométrique Révolutionnaire
Au-delà de la formule n³, découvrez la structure hexagonale des nombres cubiques
Une Révolution Conceptuelle
Cette approche transcende la vision purement académique des nombres cubiques comme simple multiplication n × n × n.
La Découverte Fondamentale
Les nombres cubiques émergent naturellement de l'addition successive des nombres hexagonaux centrés, révélant une structure géométrique profonde que les mathématiques traditionnelles occultent.
Vision non-académique : Chaque nombre cubique contient en lui la mémoire de tous les hexagones centrés qui l'ont précédé, créant une spirale de croissance organique.
Implications Spirituelles
Cette représentation 2D du déploiement hexagonal nous montre que :
- La croissance cubique suit des lois harmoniques
- L'expansion suit un pattern hexagonal sacré
- Chaque étape contient la totalité du processus
Cette vision unifie géométrie plane et volume dans une synthèse qui dépasse la fragmentation des disciplines académiques.
Nombres Étoilés : L'Homothétie Interne des Nombres Cubiques
Quand l'étoile contient totalement sa précédente : la révélation des puissances de 2
L'Homothétie Stellaire des Nombres Cubiques
Le Principe d'Homothétie Interne
Chaque étoile contient totalement sa précédente selon une homothétie interne parfaite. Ce moment précis d'inclusion complète marque l'émergence d'un nouveau pallier de nombres cubiques.
La Loi des Puissances de 2
Les nombres étoilés correspondant à ce pattern d'homothétie interne suivent rigoureusement les puissances de 2 :
Pattern découvert : 2¹, 2², 2³, 2⁴... Chaque puissance de 2 correspond à un moment d'inclusion stellaire totale, générant le pallier cubique suivant.
Révélation Structurelle
Cette découverte dévoile que :
- L'expansion cubique suit une logique d'emboîtement stellaire
- Les puissances de 2 marquent les seuils d'inclusion totale
- Chaque pallier cubique émerge d'une homothétie parfaite
- La croissance n³ cache une architecture d'emboîtements successifs
Vision Unifiée
Cette approche révèle l'unité profonde entre géométrie planaire (étoiles), progression exponentielle (puissances de 2) et expansion volumétrique (nombres cubiques). L'homothétie interne devient le principe générateur reliant ces trois dimensions mathématiques.
🎯 Explorez Votre Géométrie Personnelle
Découvrez comment les principes de la géométrie sacrée s'appliquent à votre profil numérologique unique et révèlent vos patterns énergétiques.
❓ Questions Fréquentes sur la Géométrie Sacrée
Comprendre les mystères de la géométrie créatrice
Qu'est-ce qui rend une géométrie "sacrée" ?
+Une géométrie est considérée comme sacrée quand elle révèle des principes universels qui régissent la création.
Pourquoi n'y a-t-il que trois pavages réguliers possibles ?
+Mathématiquement, seuls les polygones dont les angles internes permettent de totaliser exactement 360° autour d'un point peuvent paver le plan.
🔢 Les trois pavages possibles :
Triangle (60°×6) | Carré (90°×4) | Hexagone (120°×3)
Comment les trois figures mères correspondent-elles aux aspects de l'être ?
+Cette correspondance reflète la constitution ternaire de l'être humain selon les traditions spirituelles :
Esprit, intellect
Âme, émotions
Corps, matière
Que sont les grilles de construction de Franz Rziha ?
+Ce sont des matrices géométriques découvertes dans l'analyse des marques de tailleurs de pierre médiévaux.
Elles révèlent que tous les symboles dérivent de ces quelques matrices fondamentales.
