LES CHIFFRES DE LA NUMÉROLOGIE

Les 9 nombres-réduits et les 29 nombres-sources

LES NEUF CHIFFRES DE LA NUMÉROLOGIE

Les chiffres de 1 à 9

Combien de chiffres utilise-t-on en numérologie

123456789

En numérologie, les nombres 11 et 22 sont appelés "nombres maîtres". Ces nombres sont considérés comme très puissants et porteurs d'une signification spéciale en raison de leur nature double. En d'autres termes, les nombres 11 et 22 sont des nombres qui ne sont pas réduits à un seul chiffre car ils ont une signification unique en eux-mêmes.

Nous avons vu dans la partie consacrée à la numérologie que cette appelation était pour le moins fantaisiste.

par contre les nombres 11 et 20 font bien partie des 29 nombres-source de la géo-numérologie.

Le nombre 11 est souvent associé à l'illumination spirituelle et à la compréhension intuitive profonde. Les personnes qui ont un nombre de vie ou un nombre d'expression 11 sont souvent très intuitives, sensibles et ont une capacité naturelle à ressentir les émotions et les énergies des autres.

Ils peuvent être des médiums, des guérisseurs ou des enseignants spirituels. Les personnes ayant un nombre de vie ou un nombre d'expression 11 sont souvent appelées à développer leur spiritualité et leur conscience spirituelle tout au long de leur vie.

Le nombre 22 est souvent associé à la capacité de manifester des idées et des projets dans le monde matériel. Les personnes qui ont un nombre de vie ou un nombre d'expression 22 sont souvent très créatives et ont une vision claire de ce qu'elles veulent accomplir dans la vie.

Ils ont une capacité naturelle à organiser et à structurer des projets de grande envergure et à les mener à bien.

Plus généralement nous verrons plus loin que les nombres doubles peuvent indiquer des défis et des obstacles plus importants. Les personnes ayant des nombres doubles dans leur profil numerologique peuvent donc être appelées à relever des défis plus difficiles pour atteindre leur plein potentiel.

Les 9 nombres-réduits

Les nombres de la numérologie

Le nombre 1 peut être associé à l'indépendance, la force et la confiance en soi, qui peuvent être considérés comme des qualités liées à la vertu de la courage.
Le nombre 2 peut être associé à la diplomatie, la coopération et l'empathie, qui peuvent être considérés comme des qualités liées à la vertu de la bonté.
Le nombre 3 peut être associé à la créativité, l'expression et l'optimisme, qui peuvent être considérés comme des qualités liées à la vertu de la joie.
Le nombre 4 peut être associé à la stabilité, la persévérance et la responsabilité, qui peuvent être considérés comme des qualités liées à la vertu de la diligence.
Le nombre 5 peut être associé à la liberté, la curiosité et l'aventure, qui peuvent être considérés comme des qualités liées à la vertu de la courage.
Le nombre 6 peut être associé à l'harmonie, la paix et la protection, qui peuvent être considérés comme des qualités liées à la vertu de la générosité.
Le nombre 7 peut être associé à la recherche de la connaissance, la compréhension et la spiritualité, qui peuvent être considérés comme des qualités liées à la vertu de la sagesse.
Le nombre 8 peut être associé à l'autorité, la puissance et la richesse, qui peuvent être considérés comme des qualités liées à la vertu de la générosité.
Le nombre 9 peut être associé à la philanthropie, la compassion et la tolérance, qui peuvent être considérés comme des qualités liées à la vertu de la miséricorde.

LES 29 NOMBRES DE LA GÉO-NUMÉROLOGIE

Les 29 archétypes de personnalité

Classification des 29 nombres sources

Mondes et Attributs

Dans le schéma ci-contre les 29 nombres-source de la géonumérologie sont classés selon leur degré d'intégration.

On distingue d'abord trois catégories selon l'appartenance à un, deux ou trois Mondes. Puis on regarde la couleur des Attributs présents.

On obtient la classification suivante :

Nombres présents dans un seul Monde ...
- ... et dotés d'un seul type d'Attribut : 10, 20, 30, 40, 50, 60, 70, 80 et 90
- ... et dotés de deux types d'Attribut : 11
- ... et dotés de trois types d'Attribut : 12
Nombres présents dans deux Mondes ...
- ... et dotés d'un seul type d'Attribut : 33
- ... et dotés de deux types d'Attribut : 13, 14, 17, 22, 23 et 44
- ... et dotés de trois types d'Attribut : 15, 18, 24, 27 et 45
Nombres présents dans trois Mondes ...
- ... et dotés d'un seul type d'Attribut : 36
- ... et dotés de deux types d'Attribut : 16, 25, 26, 34 et 35
- ... et dotés de trois types d'Attribut : aucun

La roue des nombres

Des 4 valeurs secrètes à l'ensemble des nombres

Dans la roue ci-contre sont positionnées au centre les 4 valeurs secrètes : 1, 3, 6 et 9.

A chaque valeur secrète est associé les nombres-réduits correspondant (cercle médian).

A chaque nombre réduit sont associés les nombres-source correspondants (cercle périphérique).

On peut ainsi connaître d'un coup d'oeil la valeur secrète d'un nombre-source (sans passer par l'addition et la réduction).

Par exemple les nombres sources 10, 13, 22, 40, 16, 25, 34 et 70 ont tous une valeur secrète de 1.

Cette roue permet l'interprétation de n'importe quel nom/nombre.

Prenons le prénom christophe, de valeur numérique 58. Pour savoir où le positionner dans la roue, il suffit de faire la réduction de 58, soit 5 + 8 = 13.

Le nombre 58 appartient donc à la famille des nombres-source 13, ayant pour réduction le nombre 4 et la valeur secrète 1.

CE QU'IL FAUT RETENIR

9 Nombres Réduits, 29 Nombres-Source et 4 Valeurs secrètes.

Numérologie 6/8

Les 3 points-clefs

Les neuf nombres de la numérologie s'obtiennent à travers 29 nombres-source qui représentent l'extension du concept de maître-nombre à tous les chiffres.

9Les 9 Nombres Réduits : En numérologie, chaque nombre de 1 à 9 possède des attributs et des vertus spécifiques. Le nombre 1 est associé à l'indépendance et la force, symbolisant la vertu du courage. Le 2 représente la diplomatie et l'empathie, reflétant la bonté. Le 3, lié à la créativité et l'optimisme, incarne la joie. Le 4 symbolise la stabilité et la responsabilité, évoquant la diligence. Le 5, associé à la liberté et l'aventure, représente également le courage. Le 6, relié à l'harmonie et la protection, traduit la générosité. Le 7, symbolisant la quête de connaissance, est connecté à la sagesse. Le 8, représentant l'autorité et la richesse, est lié à la générosité. Enfin, le 9, associé à la philanthropie et la compassion, représente la miséricorde.

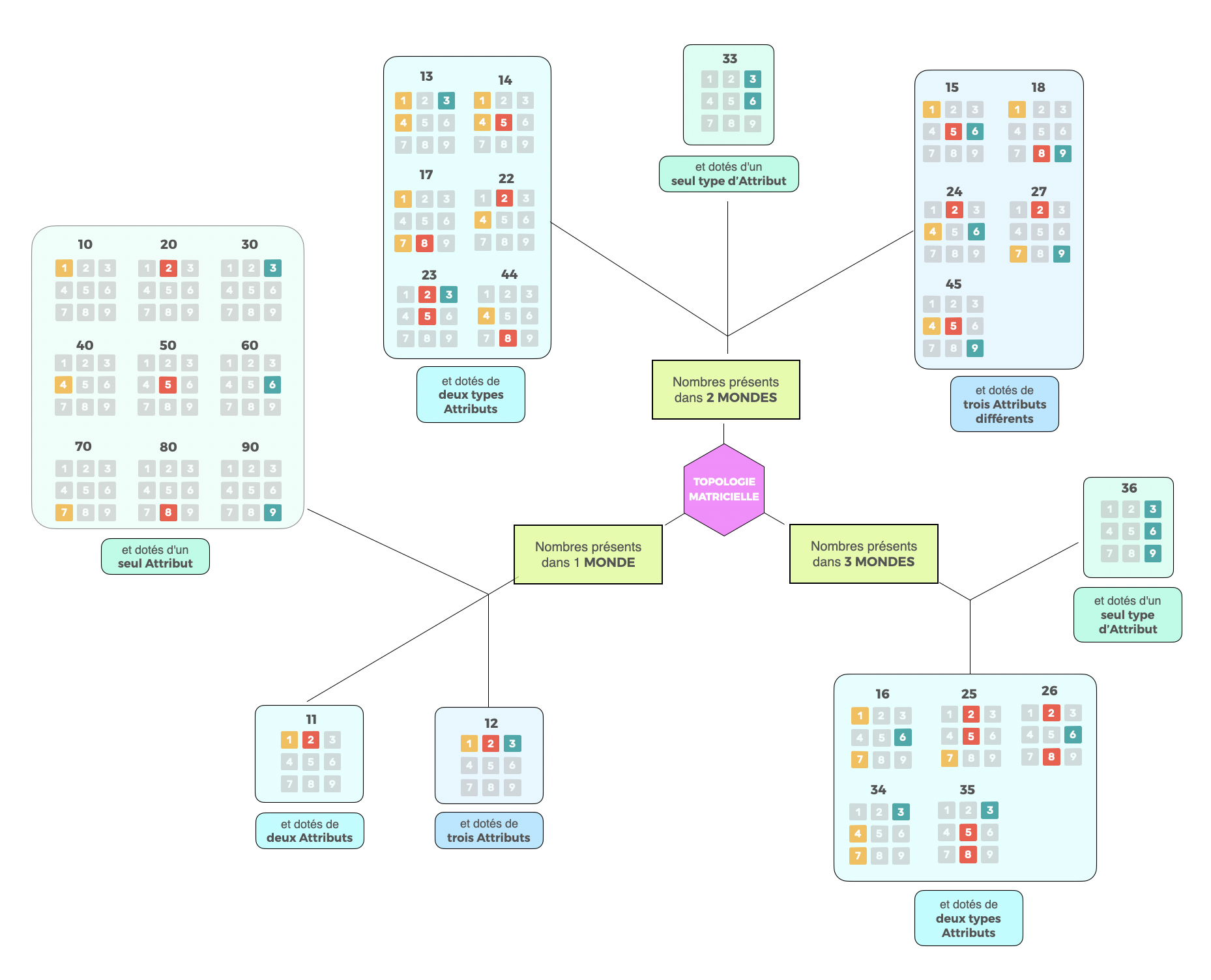
29Les 29 Nombres Source : La Géonumérologie s'inntéresse à la manière d'obtenir les 9 premiers nombres. Il existe 29 nombres-source à l'origine des 9 nombres-réduits. C'est le principe de base de la Géo-Numérologie (Cf plus loin). Chaque individu possède au maximum 5 symboles personnels, constituant chacun, une parcelle de la personnalité. Leur degré de composition permet de les distinguer les uns des autres et notamment à travers la localisation du chiffre et de ses composants dans la matrice des neuf nombres.

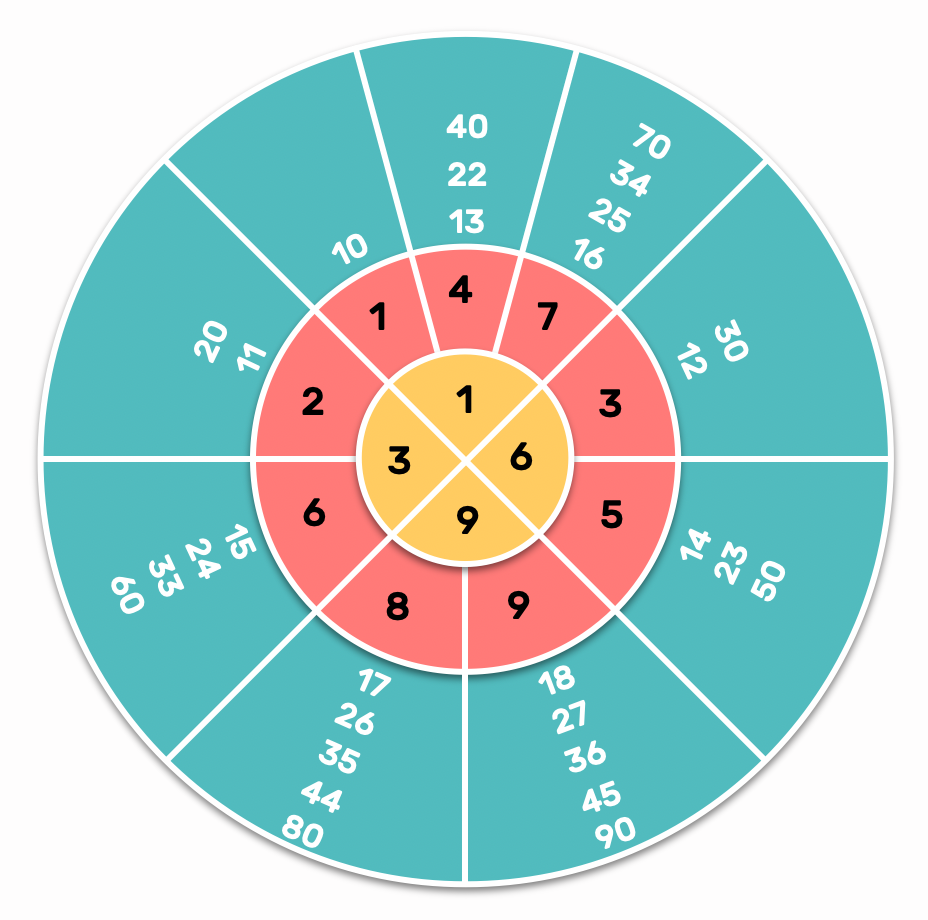
6Les Nombres Secrets 1369 : Au cœur de la Géonumérologie se trouvent les quatre valeurs secrètes : 1, 3, 6 et 9. Ces nombres sont positionnés au centre de la roue des nombres, entourés par les nombres-réduits correspondants et leurs nombres-source associés. Cette disposition offre une vision globale de la relation entre les valeurs secrètes, les nombres-réduits et les nombres-source, permettant une interprétation rapide et intuitive des caractéristiques profondes d'un nombre sans recourir à des calculs complexes.