📖 Sommaire
- La Tri-Unité Originelle
- Construction du Triangle
- La Tetraktys de Pythagore
- Les 6 Diagonales — Du Point à l'Hyperdimension
- Géométrie Combinatoire
- Simplexes Hyperdimensionnels (4D → 7D)
- Triangle de Pascal et Jeu de Dés
- Les Nombres 153 et 666
- Le Triangle de Sierpinski
- Ce qu'il faut retenir
- Vidéos : Triangle de Pascal
- Questions fréquentes
La Tri-Unité Originelle
« Chaque nombre est la somme des deux nombres au-dessus de lui »
📐 Origine historique
Le triangle de Pascal tient son nom de Blaise Pascal, auteur du Traité du Triangle Arithmétique (1654).
Cependant, il était déjà connu des mathématiciens arabes du Xe siècle et on retrouve sa trace en Chine au XIe siècle. Il apparaît dans le Miroir de jade des quatre éléments de Zhu Shijie en 1303.
Principe : Les extrémités sont toujours des 1. Les autres nombres sont la somme des deux nombres directement au-dessus.
📋 Fiche Technique
| Origine | Chine XIe s. / France 1654 |
| Symbolisme | Tri-unité, Tarot, jeu de dés |
| Archétype | Addition théosophique, puissances de 2 |
| Géométrie | Nombres triangulaires et polytopes |
| Ésotérisme | Nombres bibliques 153, 666, Tetraktys |
| Applications | Probabilités, combinatoire, fractales |
Construction du Triangle
Chaque nombre est la somme des deux nombres au-dessus
🔺 La Tri-Unité Originelle
Au sommet du Triangle, trois 1 forment une trinité fondamentale : le premier 1 engendre les deux 1 de la ligne suivante.
Cette tri-unité originelle est la source de tous les nombres du Triangle. Par simple addition des deux nombres supérieurs, elle génère l'infini des combinaisons possibles.
Le miracle : Trois unités suffisent à engendrer tous les types de nombres — triangulaires, tétraédriques, pentatopiques... jusqu'à l'hyperdimension.
Les cellules ■ cyan contiennent des 1 — la diagonale de l'unité qui borde le Triangle à l'infini.
1. La Tetraktys de Pythagore
« Par la Tetraktys, source de l'éternelle Nature ! »
La Tetraktys pythagoricienne n'est autre que les 4 premières lignes du Triangle de Pascal. C'était le symbole sacré sur lequel les Pythagoriciens prêtaient serment.
🔺 Correspondances
| Ligne 1 | 1 point | Monade — Feu | H 1 |
| Ligne 2 | 2 points | Dyade — Air | O 2 |
| Ligne 3 | 3 points | Triade — Eau | N 3 |
| Ligne 4 | 4 points | Tétrade — Terre | C 4 |
Couches électroniques : Les nombres 1, 2, 3, 4 correspondent au nombre d'électrons nécessaires pour combler les sous-couches s, p, d, f de l'atome. Les 4 atomes de la Vie (H, O, N, C) suivent ainsi la Tetraktys dans leur capacité de liaison.
Les 6 Diagonales — Du Point à l'Hyperdimension
« Chaque diagonale correspond à une dimension de l'espace »
Signification : Le Point — élément sans dimension
1, 1, 1, 1, 1, 1...
Signification : La Ligne — formée par 2 points
1, 2, 3, 4, 5, 6, 7...
Signification : Le Triangle — 3 points, 3 lignes
1, 3, 6, 10, 15, 21, 28...
Signification : Le Tétraèdre — 4 points, 4 faces triangulaires
1, 4, 10, 20, 35, 56, 84...
Signification : Le Pentachore — 5 sommets, 5 cellules tétraédriques
1, 5, 15, 35, 70, 126...
Signification : Le 5-Simplexe — 6 sommets, 6 cellules 4D
1, 6, 21, 56, 126, 252...
Principe d'emboîtement : Chaque famille est la somme cumulative de la précédente. C'est la progression dimensionnelle infinie.
Géométrie Combinatoire
Du nombre à la forme : figurer les coefficients binomiaux
📊 Sous-ensembles par ligne
- n=1 : 1, 1 point
- n=2 : 1, 2 points, 1 ligne
- n=3 : 1, 3 points, 3 lignes, 1 triangle
- n=4 : 1, 4 points, 6 lignes, 4 △, 1 tétra
- n=5 : 1, 5 points, 10 lignes, 10 △, 5 tétra, 1 penta
🔑 La Clé : Le nombre de points = le nombre de volumes (n-1).
Le Pentachore a 5 points ET 5 tétraèdres comme faces. Cette symétrie révèle la structure profonde de l'hyperdimension.
⚡ Puissances de 2
La somme de chaque ligne donne 2ⁿ, le nombre total de sous-ensembles (y compris l'ensemble vide) :
- n=1 → 1+1 = 2 = 2¹
- n=2 → 1+2+1 = 4 = 2²
- n=3 → 1+3+3+1 = 8 = 2³
- n=4 → 1+4+6+4+1 = 16 = 2⁴
- n=5 → 1+5+10+10+5+1 = 32 = 2⁵
Les Simplexes Hyperdimensionnels
Du Tétraèdre au 7-Simplexe — La construction par itération
Un simplexe en dimension n se construit en ajoutant un nouveau sommet à un simplexe de dimension n-1. Cette construction révèle une symétrie fondamentale : le nombre de sommets égale le nombre de cellules (n-1).
Pentachore (5-cell) : un tétraèdre central + 4 tétraèdres collés sur chaque face
| Dimension | Nom | Sommets | Cellules (n-1) | Ligne Pascal | Total éléments |
|---|---|---|---|---|---|
| 2D | Triangle | 3 | 3 lignes | 1, 3, 3, 1 | 8 = 2³ |
| 3D | Tétraèdre | 4 | 4 triangles | 1, 4, 6, 4, 1 | 16 = 2⁴ |
| 4D | Pentachore (5-cell) | 5 | 5 tétraèdres | 1, 5, 10, 10, 5, 1 | 32 = 2⁵ |
| 5D | Hexatéron (5-simplexe) | 6 | 6 pentachores | 1, 6, 15, 20, 15, 6, 1 | 64 = 2⁶ |
| 6D | Heptatéron (6-simplexe) | 7 | 7 hexatérons | 1, 7, 21, 35, 35, 21, 7, 1 | 128 = 2⁷ |
| 7D | Octatéron (7-simplexe) | 8 | 8 heptatérons | 1, 8, 28, 56, 70, 56, 28, 8, 1 | 256 = 2⁸ |
🔑 La Symétrie Fondamentale
Pour tout n-simplexe : Nombre de sommets = Nombre de cellules (n-1) = n + 1
Progression dimensionnelle des simplexes : du tétraèdre 3D au heptatéron 6D
🔺 Famille Triangulaire (Σ)
Les nombres figurés suivent la logique cumulative :
- Triangulaires : 1, 3, 6, 10, 15...
- Tétraédriques : 1, 4, 10, 20, 35...
- Pentatopiques : 1, 5, 15, 35, 70...
Hexaédriques (6ème diagonale) :
Chaque terme = somme des termes précédents de la série précédente.
🔲 Famille Cubique (×2)
Les sommets des hypercubes suivent le doublement :
- Point : 1 sommet
- Ligne : 2 sommets
- Carré : 4 sommets
- Cube : 8 sommets
- Tesseract : 16 sommets
Chaque terme = 2 × le terme précédent.
🌉 Le Pont : Les Simplexes unissent les deux familles
Le total des éléments d'un n-simplexe (sommets + arêtes + faces + ...) égale 2ⁿ⁺¹.
La somme de la ligne n+1 du Triangle de Pascal !
Triangle de Pascal et Jeu de Dés
Les nombres 1, 6, 21, 56 — La 6ème diagonale
1 face
6 faces
21 combinaisons
56 combinaisons
🎲 Combinaisons uniques avec n dés
Les nombres de la 6ème diagonale : 1, 6, 21, 56, etc. correspondent aux nombres de combinaisons uniques avec un jeu comportant n dés.
🎲 Avec 1 dé : 6 possibilités différentes
⚀ ⚁ ⚂ ⚃ ⚄ ⚅
🎲🎲 Avec 2 dés : 6 × 6 = 36 possibilités
Après retrait des doublons (⚀⚁ = ⚁⚀) → 21 uniques
🎲🎲🎲 Avec 3 dés : 6 × 6 × 6 = 216 possibilités
→ 56 combinaisons uniques
🃏 Lien avec le Tarot de Marseille
Remarquez que les nombres 21 et 56 sont également :
- 21 = Arcanes Majeurs (sans le Mat/Fou)
- 56 = Arcanes Mineurs du Tarot
Le Jeu des Vertus : L'évêque Wibold de Cambrai inventa ce jeu pour les moines au Xe siècle. Le but : acquérir des « vertus » à l'aide de 3 dés. Il existe 56 vertus, soit exactement le nombre de combinaisons uniques avec trois dés !
🔮 Tarot et Nombres Tétraédriques 5D
La 6ème diagonale du Triangle de Pascal révèle une correspondance remarquable avec la structure du Tarot :
| Nombre | Formule | Tarot |
|---|---|---|
| 21 | T(6) = C(7,2) | Arcanes Majeurs (sans Mat) |
| 56 | C(8,3) | Arcanes Mineurs |
| 78 | T(12) = 12ème triangulaire | Tarot complet (22 + 56) |
Les nombres de la 6ème diagonale encodent la structure même du Tarot de Marseille, suggérant un lien profond entre combinatoire et divination.
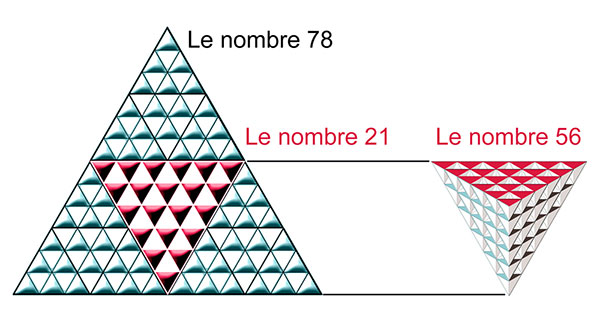
Le patron du tétraèdre : 4 faces de 21 = 78 cartes
Les Nombres 153 et 666
Nombres triangulaires et symbolisme biblique
153
🐟 Les Poissons de Jean
« Simon Pierre monta dans la barque, et tira à terre le filet plein de cent cinquante-trois grands poissons. »
— Jean 21:11
153 = 17ème nombre triangulaire
= Nombre de lignes parmi 18 points
18 points = la couronne périphérique de la Fleur de Vie (la 3ème couronne contient 18 cercles).
Le mot filet (du latin rete) signifie aussi maillage, réseau — exactement comme les lignes connectant les points de la Fleur de Vie.
666
😈 Le Nombre de la Bête
« Que celui qui a de l'intelligence calcule le nombre de la bête. Car c'est un nombre d'homme, et son nombre est six cent soixante-six. »
— Apocalypse 13:18
666 = 36ème nombre triangulaire
= Nombre de lignes parmi 37 points
37 points = la Fleur de Vie complète (1 centre + 6 + 12 + 18 = 37 stations).
Le "nombre de la Bête" représente en réalité le maillage complet de la Fleur de Vie — toutes les connexions possibles entre ses 37 centres.
🔗 La Clé : 18 et 37
Pour comprendre ces énigmes bibliques, il faut se concentrer sur les nombres à l'origine de ces "connexions divines" :
- 18 = 3ème couronne de la Fleur de Vie → 153 lignes possibles
- 37 = Fleur de Vie complète → 666 lignes possibles
Ces nombres représentent le nombre de relations binaires (lignes, liens) qu'il est possible de former dans un ensemble de n éléments.
Le Triangle de Sierpinski
Pascal modulo 2 = Structure fractale — Les puissances de 3
Si l'on colorie en noir les nombres impairs et en blanc les nombres pairs du Triangle de Pascal, on obtient le Triangle de Sierpinski — une fractale auto-similaire.
Auto-similarité ternaire : Le triangle contient 3 copies de lui-même à chaque niveau de zoom. C'est la manifestation géométrique de la loi ternaire dans la structure même des nombres.
À chaque itération, le nombre de triangles est multiplié par 3 :
- 3⁰ = 1 triangle initial
- 3¹ = 3 triangles
- 3² = 9 triangles
- 3³ = 27 triangles
- 3⁴ = 81 triangles
- etc.
Ce qu'il faut retenir
🔢 Nombres
Les diagonales encodent toutes les familles de nombres figurés : entiers, triangulaires, tétraédriques, et au-delà vers l'hyperdimension.
📐 Géométrie
Les coefficients binomiaux comptent les sous-structures : points, lignes, triangles, tétraèdres. La géométrie combinatoire en action.
✨ Symbolisme
Tetraktys, Tarot, jeu de dés, nombres bibliques 153 et 666, fractale de Sierpinski — la « combinatoire de Dieu ».
🎬 Le Triangle de Pascal en Vidéo
« La Combinatoire de Dieu »
Deux explorations visuelles des mystères du triangle
🔢 Triangle de Pascal et Combinatoire
Points clés :
- C Les coefficients binomiaux C(n,k)
- 🎲 Calcul des probabilités
- Σ Les puissances de 2 (somme des lignes)
📐 Triangles en n-Dimensions
Points clés :
- △ Du triangle au tétraèdre
- ⬡ Les simplexes en 4D, 5D...
- ∞ L'hyperdimension dans les diagonales
« Le Triangle de Pascal est une structure fractale qui contient en elle-même les clés de toutes les dimensions. »
❓ Questions Fréquentes sur le Triangle de Pascal
Comprendre la combinatoire divine
Pourquoi les extrémités du triangle sont-elles toujours 1 ?
+Les extrémités représentent les coefficients binomiaux C(n,0) et C(n,n), qui valent toujours 1 : il n'y a qu'une seule façon de choisir 0 élément ou tous les éléments parmi n.
Quel est le lien entre Pascal et Sierpinski ?
+En coloriant les nombres impairs du Triangle de Pascal, on obtient exactement le Triangle de Sierpinski. Cela révèle que la structure fractale ternaire est « cachée » dans les propriétés arithmétiques du triangle.
Comment les nombres 153 et 666 sont-ils liés à la Fleur de Vie ?
+153 est le nombre de lignes (connexions) entre les 18 points de la 3ème couronne de la Fleur de Vie.
666 est le nombre de lignes entre les 37 points de la Fleur de Vie complète.
Ces nombres triangulaires représentent le « maillage » de la structure sacrée.
Pourquoi 21 et 56 apparaissent dans le Tarot ?
+Ces nombres de la 6ème diagonale (1, 6, 21, 56...) correspondent aux combinaisons uniques avec des dés :
- 21 = combinaisons uniques avec 2 dés = 21 Arcanes Majeurs
- 56 = combinaisons uniques avec 3 dés = 56 Arcanes Mineurs
Le Tarot semble encodé dans la structure même du hasard !
