📖 Sommaire
1. La Géométrie des Nombres
Les nombres figurés révèlent l'unité profonde
entre l'arithmétique et la géométrie.
Qu'est-ce qu'un Nombre Figuré ?
Les nombres figurés sont des nombres entiers représentables par des points disposés selon une figure géométrique régulière.
Cette approche pythagoricienne révèle les liens profonds entre arithmétique et géométrie. Chaque famille possède deux particularités remarquables :
- Croissance Fractale : les nombres croissent en conservant la similitude de forme (autosimilarité)
- Construction Géométrique : chaque nombre peut être construit avec des points ou la figure mère
« Or, ainsi qu'il a été dit au commencement, tout était en désordre, quand Dieu introduisit des proportions en toutes choses, dans toute la mesure qu'elles admettaient la proportion et la symétrie. » — Platon, Le Timée
Les Trois Familles Universelles
Au-delà de la 4ème dimension, seules trois familles de polytopes réguliers se prolongent dans toutes les dimensions :
△
SIMPLEXES
Triangle → Tétraèdre → Pentachoron...
(n+1 sommets)
⬜
HYPERCUBES
Carré → Cube → Tesseract...
(2ⁿ sommets)
◇
ORTHOPLEXES
Carré → Octaèdre → Hexadécachore...
(2n sommets)
Ces trois familles sont encodées dans le Triangle de Pascal : les simplexes dans ses diagonales, les hypercubes dans les sommes de lignes (2ⁿ).
2. Les 10 Familles de Nombres Figurés
Vue d'ensemble des séquences et de leurs propriétés
| N° | Famille | Dim. | Séquence | Création | Figure |
|---|---|---|---|---|---|
| 1 | Entiers | 1D | 1, 2, 3, 4, 5, 6, 7, 8, 9... | Base | • |
| 2 | Triangulaires | 2D | 1, 3, 6, 10, 15, 21, 28... | Σ entiers | △ |
| 3 | Tétraédriques | 3D | 1, 4, 10, 20, 35, 56... | Σ triangulaires | △ |
| 4 | Hyper-tétra 4D | 4D | 1, 5, 15, 35, 70, 126... | Σ tétraédriques | △ |
| 5 | Hyper-tétra 5D | 5D | 1, 6, 21, 56, 126, 252... | Σ hyper-tétra 4D | △ |
| 6 | Hexagonaux | Treillis | 1, 6, 12, 18, 24, 30... | Grille de base | ⬡ |
| 7 | Hexa centrés (Flora) | 2D | 1, 7, 19, 37, 61, 91... | Σ hexagonaux | ⬡ |
| 8 | Cubiques | 3D | 1, 8, 27, 64, 125, 216... | Σ hexa centrés | ⬡ |
| 9 | Hypercubes 4D | 4D | 1, 16, 81, 256, 625... | n⁴ | ⬡ |
| 10 | Étoilés | 2D | 1, 13, 37, 73, 121... | Flora + 6×triangulaires | ✡ |
3. Les Nombres Triangulaires
Archétype des formes 2D • La Tetraktys de Pythagore
| n° (rang) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Entiers naturels | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Triangulaires | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
Fiche Technique
| Dimension | 2D |
| Séquence | 1, 3, 6, 10, 15, 21... |
| Création | Σ des entiers |
| Formule | n(n+1)/2 |
| Figure | Triangle △ |
| Clé | 10 = Tetraktys |
Les nombres triangulaires s'obtiennent par addition successive des entiers :
| Σ entiers | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Addition | 1 | 1+2 | +3 | +4 | +5 | +6 |
| Triangulaire | 1 | 3 | 6 | 10 | 15 | 21 |
Le nombre 10, quatrième triangulaire, est la célèbre Tetraktys de Pythagore.
« J'en jure par celui qui grava dans nos cœurs la Tétrade sacrée, immense et pur symbole, Source de la Nature, et modèle des Dieux. » — Serment pythagoricien
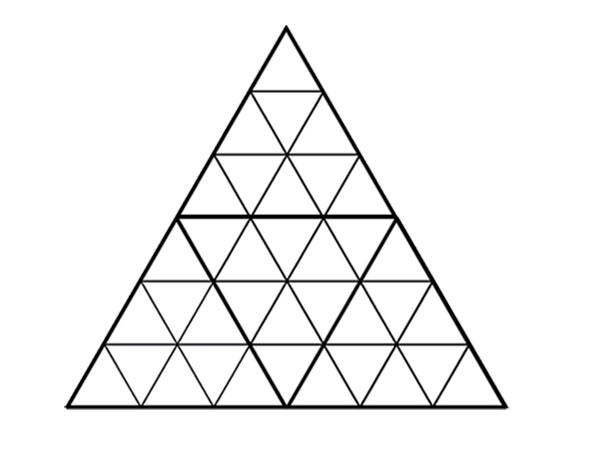
(unité de mesure : point)
📖 Symbolisme Biblique : 153 et 666
🐟 Les 153 Poissons (Jean 21:11)
153 est le 17ème triangulaire. Il correspond aux connexions entre 18 points — les 18 stations périphériques de la Fleur de Vie.
😈 Le Nombre 666 (Apoc. 13:18)
666 est le 36ème triangulaire. Il correspond aux connexions entre les 37 stations de la Fleur de Vie.
☞ Ce n'est pas au rang qu'il faut s'intéresser mais au nombre générateur : 18 et 37.
4. Les Nombres Tétraédriques
Archétype des formes 3D • Du plan au volume
| n° (rang) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Triangulaires | 1 | 3 | 6 | 10 | 15 | 21 | 28 |
| Tétraédriques | 1 | 4 | 10 | 20 | 35 | 56 | 84 |
| Pentatopiques | 1 | 5 | 15 | 35 | 70 | 126 | 210 |
Fiche Technique
| Dimension | 3D |
| Séquence | 1, 4, 10, 20, 35, 56... |
| Création | Σ des triangulaires |
| Formule | n(n+1)(n+2)/6 |
| Figure | Tétraèdre |
| Symbole | Feu (Platon) |
Les nombres tétraédriques s'obtiennent par addition des triangulaires :
| n° (rang) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Σ triang. | 1 | 1+3 | +6 | +10 | +15 |
| Tétraédrique | 1 | 4 | 10 | 20 | 35 |
De même que le triangle est la première figure fermée en 2D, le tétraèdre est le premier volume en 3D.
Le nombre 10 est remarquable : il est à la fois le 4ème triangulaire ET le 3ème tétraédrique.
- 3 points définissent un plan (triangle)
- 4 points définissent un volume (tétraèdre)

5. Les Nombres Hexagonaux
La Matrice de l'Espace-Temps • Le Treillis Universel
| n° (rang) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Hexa treillis | 1 | 6 | 12 | 18 | 24 | 30 | 36 |
| Flora (Σ hexa) | 1 | 7 | 19 | 37 | 61 | 91 | 127 |
| Cubiques (Σ Flora) | 1 | 8 | 27 | 64 | 125 | 216 | 343 |
Hexagonaux (Treillis)
| Dimension | Treillis |
| Séquence | 1, 6, 12, 18, 24, 30... |
| Création | Grille de base |
| Rôle | Matrice spatiale |
| Figure | Hexagone ⬡ |
Hexa Centrés (Flora)
| Dimension | 2D |
| Séquence | 1, 7, 19, 37, 61, 91... |
| Création | Σ des hexagonaux |
| Formule | 3n(n-1)+1 |
| Clé | 37 = Fleur de Vie |
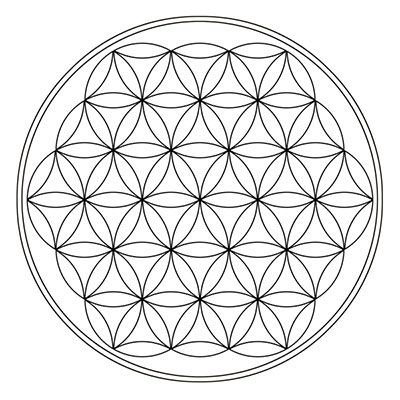
🌸 Le Treillis Hexagonal et la Fleur de Vie
Les nombres hexagonaux servent de grille ou treillis pour la construction géométrique de tous les nombres figurés du Monde Naturel.
Les nombres hexagonaux centrés (Flora) correspondent à la structure numérique de la Fleur de Vie.
La Fleur de Vie correspond au 4ème nombre Flora : 37.
- Série hexagonale : extension en ampleur
- Nombres Flora : tracés intensificateurs
- Nombres cubiques : densification matérielle
6. Les Nombres Cubiques
De la 3D à la 4D • Le Cube et l'Hypercube
| n° (rang) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Flora | 1 | 7 | 19 | 37 | 61 | 91 |
| Cubiques (Σ Flora) | 1 | 8 | 27 | 64 | 125 | 216 |
| Hypercubiques (n⁴) | 1 | 16 | 81 | 256 | 625 | 1296 |
Cubiques (3D)
| Dimension | 3D |
| Séquence | 1, 8, 27, 64, 125... |
| Création | Σ des hexa centrés |
| Formule | n³ |
| Figure | Cube |
Hypercubiques (4D)
| Dimension | 4D |
| Séquence | 1, 16, 81, 256, 625... |
| Création | Puissance n⁴ |
| Formule | n⁴ |
| Nom | Tesseract |
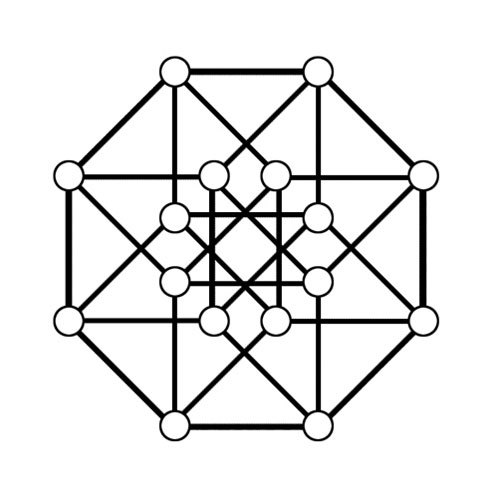
🧊 Du Cube au Tesseract
Relations entre nombres cubiques et hypercubiques :
| n° (rang) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Cubique (n³) | 1 | 1+7 | +19 | +37 | +61 |
| Hypercubiques (n⁴) | 1 | 16 | 81 | 256 | 625 |
Les nombres hypercubiques sont tous des carrés parfaits : 16 = 4², 81 = 9², 256 = 16², 625 = 25²... C'est logique : n⁴ = (n²)².
L'hypercubique de rang n est simplement le carré de n², c'est-à-dire le carré du carré. Ainsi, la 4ème dimension naît du carré qui se multiplie par lui-même — comme si l'espace se repliait sur lui-même pour engendrer la dimension suivante.
Pour visualiser un tesseract, imaginez un petit cube à l'intérieur d'un plus grand, dans un mouvement alterné d'expir et d'inspir.
« Vous puissiez comprendre quelle est la largeur, la longueur, la profondeur et la hauteur. » — Éphésiens 3:18
7. Les Nombres Étoilés
La Divine Matrice • Le Lego de Dieu
| n = | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Flora | 1 | 7 | 19 | 37 | 61 | 91 |
| 6 × Triang(n-1) | 0 | 6 | 18 | 36 | 60 | 90 |
| Étoilés | 1 | 13 | 37 | 73 | 121 | 181 |
Fiche Technique
| Dimension | 2D |
| Séquence | 1, 13, 37, 73, 121... |
| Création | Flora + 6×triangulaires |
| Formule | 6n(n-1)+1 |
| Figure | Étoile ✡ |
| Val. secrète | Toujours = 1 |
Les nombres étoilés s'obtiennent à partir des hexagonaux centrés (Flora) et des triangulaires :
| n = | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Flora(n) | 1 | 7 | 19 | 37 | 61 |
| + 6×T(n-1) | +0 | +6 | +18 | +36 | +60 |
| = Étoilé(n) | 1 | 13 | 37 | 73 | 121 |
Les nombres étoilés représentent l'expansion des hexagonaux centrés, qui en se condensant, créent les cubiques.
🌟 Nombres étoilés aux nombres cubiques
La Structure Absolue, éternelle et infinie par essence, ne connaît aucune limite : elle poursuit indéfiniment son déploiement à travers le temps et l’espace.
Pourtant, ce déploiement s’organise en paliers, en niveaux successifs, qui se manifestent tant par leur amplitude que par leur intensité.
L’extension fractale de l’Étoile se réalise par cycles réguliers, alternant continuellement des phases d’expansion et de contraction, comme la grande respiration du cosmos.
Pour saisir la figure en mouvement, il faut imaginer une dynamique double — à la fois centripète (cube) et centrifuge (étoile) — agissant sur l’ensemble et orchestrant leur devenir.
« Vous puissiez comprendre quelle est la largeur, la longueur, la profondeur et la hauteur. » — Éphésiens 3:18
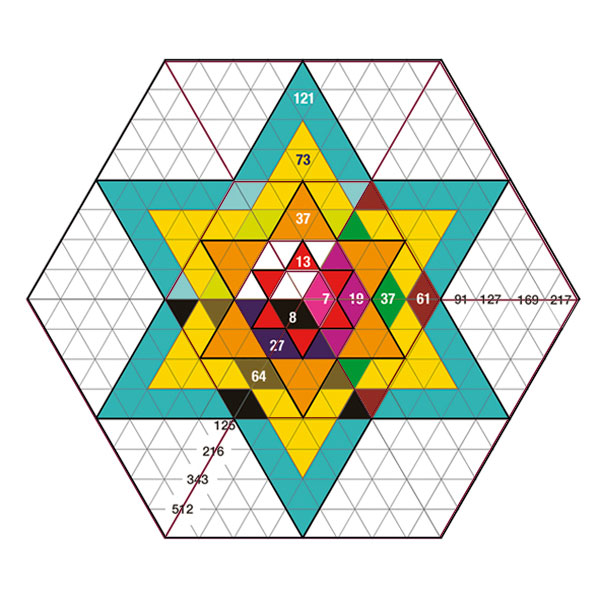
✡ Les Quatre Étoiles Majeures
Étoile 13
Ouverture du Flora 7. Intègre la Tetraktys (10), entoure le cube 8.
Étoile 37
Basée sur le Flora 19. Intègre l'étoile 13 et le triangulaire 28.
Étoile 73
Expansion du Flora 37. Composée de 6 Tetraktys.
Étoile 121
Fin de la triangulation. Englobe les étoiles 13 et 37.
Visualisation 4D/5D : Le Principe des Poupées Russes
Comment représenter les dimensions supérieures ?

🔮 Le Principe de Réduction Homothétique
Pour visualiser un polytope de dimension supérieure (4D, 5D...), chaque figure subit deux réductions homothétiques et isométriques successives :
- La figure extérieure (grande)
- La figure intermédiaire (moyenne)
- La figure intérieure (petite)
Les unes s'inscrivent dans les autres comme des poupées russes, reliées par des arêtes de connexion entre dimensions.
🎯 Vision Isotropique Centrée
Cette représentation adopte une vision isotropique centrée : l'observateur se place au centre géométrique de la figure, regardant vers l'extérieur dans toutes les directions simultanément.
C'est la perspective naturelle pour percevoir la symétrie parfaite des polytopes réguliers dans les dimensions supérieures.
🎬 Fleur de Vie et Nombres Figurés en Vidéo
« La géométrie comme langage de la création »
Comment les nombres prennent forme dans l'espace
Fleur de Vie et Nombres Figurés
🌸 De la Fleur aux Nombres
Ce que révèle cette vidéo :
Comment la Fleur de Vie encode les familles de nombres figurés
La Fleur de Vie n'est pas qu'un motif décoratif : elle contient les structures fondamentales des nombres figurés.
🔗 Points clés :
- △ Les nombres triangulaires dans les couronnes
- ⬡ Les nombres hexagonaux (1, 7, 19, 37...)
- ✡ Les nombres étoilés (1, 13, 37, 73...)
- 🔷 Les trois familles universelles au-delà de la 4D
« La géométrie est le langage dans lequel Dieu a écrit l'univers. »
— Galilée
🔮 Explorez Votre Géométrie Personnelle
Découvrez comment les principes des nombres figurés s'appliquent à votre profil numérologique unique.
❓ Questions Fréquentes sur les Nombres Figurés
Tout ce que vous devez savoir sur la géométrie des nombres
Qu'est-ce qu'un nombre figuré ?
+Un nombre figuré est un nombre entier représentable par des points disposés selon une figure géométrique régulière (triangle, carré, hexagone...).
Quelles familles de polytopes existent dans toutes les dimensions ?
+Au-delà de la 4ème dimension, seules trois familles de polytopes réguliers existent :
- 📐 Simplexes : Triangle → Tétraèdre → Pentachoron... (n+1 sommets)
- ⬜ Hypercubes : Carré → Cube → Tesseract... (2ⁿ sommets)
- ◇ Orthoplexes : Carré → Octaèdre → Hexadécachore... (2n sommets)
Les simplexes suivent une logique d'addition, les hypercubes une logique de multiplication binaire, et les orthoplexes sont les duaux des hypercubes.
Pourquoi le Triangle de Pascal est-il si important ?
+Le Triangle de Pascal encode les trois familles universelles de polytopes :
↘ Diagonales = nombres figurés des simplexes
→ Somme des lignes = sommets des hypercubes (2ⁿ)
◇ Orthoplexes = duaux des hypercubes (2n sommets)
Cette structure triangulaire (simplexe 2D) contient la clé de toute la géométrie multidimensionnelle.
Que représente la Fleur de Vie en nombres figurés ?
+La Fleur de Vie correspond au 4ème nombre hexagonal centré (Flora) : le nombre 37.
Elle représente le déploiement de l'unité dans les 6 directions de l'espace, basé sur une croissance fractale de Vesica Piscis.
